Abstract

일반적으로 K-means 알고리즘을 사용하여 비지도 군집화를 수행할 때 데이터 사이언티스트는 이미 몇 개의 군집으로 이루어져야 하는지 알고 있어야 하거나, 여러번 시행착오를 통해 군집의 개수를 감각적으로 찾을 수 밖에 없습니다. 이는 비지도 군집화의 본질적인 목적이 아니며, 이미 군집의 개수를 알고 있어야한다는 것에서 비지도의 의미가 퇴색됩니다. 스스로 이 군집의 개수를 찾아내는 방법을 학습하는 방법을 딥러닝의 생성 모델 중 하나인 Generative Adversarial Network에서의 학습 방법에서 영향을 받아 하이퍼파라미터를 조정함으로써 스스로 군집의 개수를 찾는 방법을 제시합니다.

K-means Algorithm

K-means Algorithm은 KNN 군집화와 더불어 데이터를 분석할 때 많이 사용하는 군집 알고리즘입니다. K-means Algorithm의 군집 방법을 간단히 요약하자면 다음과 같습니다. n개의 d-차원 데이터($x_1, x_2, …, x_n$)들이 주어졌을 때, n 개의 데이터들을 각 집합 내 응집도를 최대로 하는 k 개의 집합 ($S = {S_1, S_2, …, S_k}$)로 분할하는 알고리즘입니다. 이를 수식으로 표햔하면 아래와 같습니다.

\[argmin_S \Sigma^{k}_{i=0} \Sigma_{x \in S_i} || x - \mu_i||^2\]

본 글은 K-means Algorithm에 대해 고찰하는 내용이 아니므로 위의 수식에 대해 알고 싶으시면 Wikipedia에서 볼 수 있습니다.

Problem

Wikipedia에서는 K-means Algorithm에 대해 다음과 같은 한계점을 가지고 있다고 설명합니다.

클러스터 개수 k 값을 입력 파라미터로 지정해주어야 한다.
알고리즘의 에러 수렴이 전역 최솟값이 아닌 지역 최솟값으로 수렴할 가능성이 있다.
이상값에 민감하다.
구형이 아닌 크러스터를 찾는 데에는 적절하지 않다.

본 글에서는 첫번째 문제점에 집중하였습니다. NerdFactory에서 연구/개발한 AIVORY에서는 흩어져 있는 사용자들에 대해 영향을 많이 미치는 각 군집의 중심(이하 중심사용자)을 찾아야하는 문제가 있었습니다. 중심사용자를 찾기 위해서 군집화에 대한 요구가 있었으며 이를 K-means Algorithm으로 해결하였습니다. 하지만 중심사용자의 수를 찾기 위해서는 스스로 군집의 개수인 k를 탐색하는 알고리즘이 필요 했습니다.

Methodology

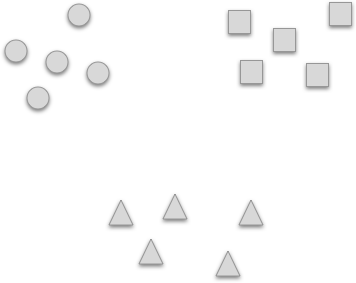
군집의 개수 k를 스스로 찾는 알고리즘을 얻기 위해서는 K-means Algorithm에 대해서 깊게 고찰할 필요가 있습니다. 고찰하는 도중 우리는 다음과 같은 개념를 얻을 수 있었습니다. 만약 실제 군집의 개수가 3인 데이터가 아래와 같이 분포되어 있다고 가정합니다.

여기서 적절한 군집을 탐색하기 위해 군집의 개수를 2부터 하나씩 늘려가며 어떤 것이 어떻게 변화하는가 지켜보았습니다.(별이 각 군집의 중심입니다.)

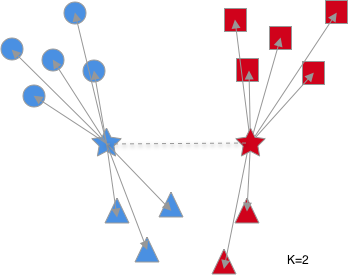
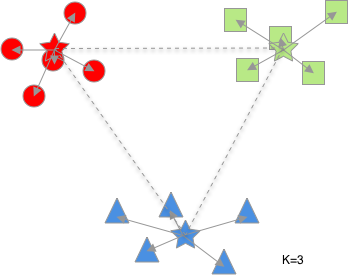
위의 그림에서 화살표는 각 군집의 중심에서 군집에 속해 있는 요소들까지의 거리이며, 점선은 각 군집의 중심 사이의 거리입니다. 군집의 개수가 증가할 수록 화살표의 길이의 합($L_1$)은 줄어드는 것을, 점선의 길이의 합($L_2$)은 증가하는 것을 알 수 있습니다. 이를 수학적으로 표현하면 아래와 같습니다. 아래의 수식에서 m은 각 군집에 속해 있는 요소의 개수입니다.

\[L_1 = \Sigma_{i=0}^{k} \Sigma_{j=0}^{m}[x_j - \mu_i]^2\] \[L_2 = \Sigma_{i=0}^{k}\Sigma_{j=0}^{k}[\mu_j - \mu_i]^2\]

위에서 k값이 증가할수록 $L_1$은 지속적으로 줄어들고, $L_2$는 지속적으로 증가하는 것을 이용합니다. k 값이 증가시키며 $L_1 + L_2$를 구해보면 지속적으로 줄어들다가 다시 증가하는 것을 볼 수 있습니다. 이는 아래로 볼록한 그래프를 가지며 최소값을 가지는 지점에서의 k 값이 최적화된 군집의 개수임을 알 수 있습니다.

여기서 $L_1$과 $L_2$의 값 사이의 비율을 정의하기 위해서 $\alpha$를 이용하여 목표함수를 다음과 같이 구합니다.

\[L_{total} = \alpha L_1 + (1-\alpha) L_2\]

그러므로 k 값을 1씩 증가시키면서 $L_{total}$이 가장 적은 k 값을 선택하면 적절한 군집의 개수라고 할 수 있습니다.

Experiment & Result

4개의 군집을 이루는 데이터를 임의적으로 생성하여 위의 알고리즘을 통했을때 군집의 개수가 4인지 알아볼 것 입니다. 생성한 데이터를 그래프화하면 아래와 같습니다.

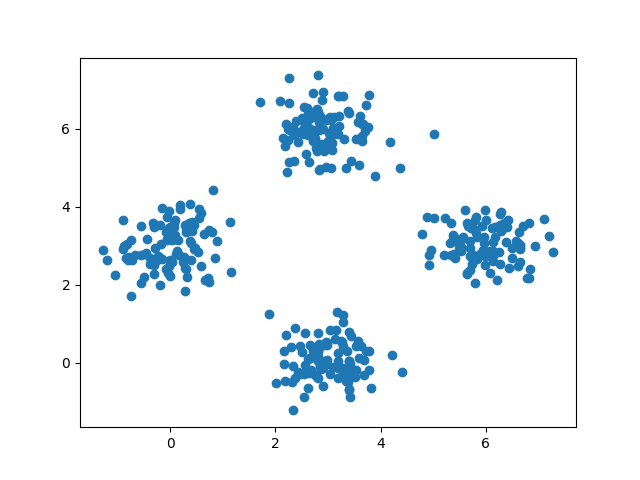
각 값을 그래프화 하면 아래와 같으며 코드는 아래에 첨부되어 있습니다.

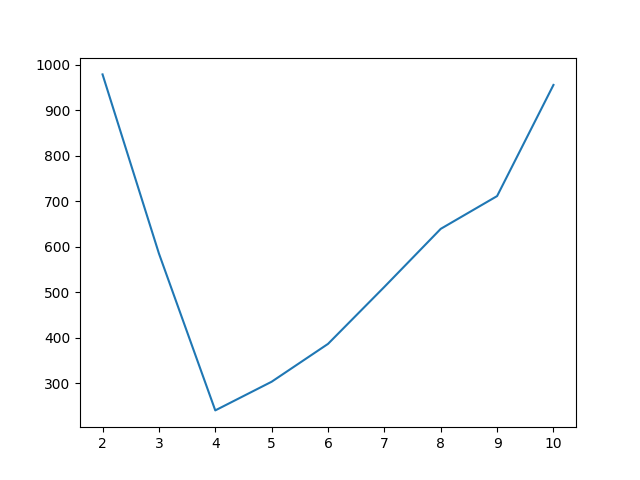
x축은 군집의 개수이며 y축은 $L_1 + L_2$ 입니다. 그래프를 보면 군집이 4개인 곳에서 가장 최저점을 나타내는 것을 볼 수 있으며 위에서 세웠던 가정과 같이 아래로 볼록한 개형을 가지는 것을 알 수 있습니다.

Code

from sklearn.cluster import KMeans
import matplotlib
matplotlib.use('TkAgg')
import matplotlib.pyplot as plt
import numpy as np

x, y = [], []

x1 = np.random.normal(3, 0.5, 100)
y1 = np.random.normal(0, 0.5, 100)

x2 = np.random.normal(0, 0.5, 100)
y2 = np.random.normal(3, 0.5, 100)

x3 = np.random.normal(6, 0.5, 100)
y3 = np.random.normal(3, 0.5, 100)

x4 = np.random.normal(3, 0.5, 100)
y4 = np.random.normal(6, 0.5, 100)

x.extend(x1)
y.extend(y1)
x.extend(x2)
y.extend(y2)
x.extend(x3)
y.extend(y3)
x.extend(x4)
y.extend(y4)

alpha = 0.5
cluster_number = 10
data = [[i, j] for i, j in zip(x, y)]
for cl in range(1, cluster_number):
    model1 = KMeans(n_clusters=cl+1, init="random", n_init=10,
               max_iter=10, random_state=1).fit(data)

    center = model1.cluster_centers_
    L1 = 0
    for i, k in zip(data, model1.labels_):
        L1 += np.dot(i-center[k],i-center[k])

    L2 = 0
    k = cl+1
    for i in range(k):
        for j in range(k):
            L2 += np.dot(center[i] - center[j], center[i] - center[j])
    print('L1:', L1, 'L2:', L2, 'L1+L2:', alpha*L1+(1-alpha)*L2, 'k:', cl+1)

Result :

L1: 1956.367718301706 L2: 36.45233981022609 L1+L2: 996.410029055966 k: 2
L1: 1043.2587384298972 L2: 128.4881979639017 L1+L2: 585.8734681968995 k: 3
L1: 172.65883469867654 L2: 288.5060699291466 L1+L2: 230.58245231391157 k: 4
L1: 153.69018256127134 L2: 438.6129661928301 L1+L2: 296.1515743770507 k: 5
L1: 136.0178456734969 L2: 667.3266662521281 L1+L2: 401.6722559628125 k: 6
L1: 124.73010013536404 L2: 892.3218260555652 L1+L2: 508.52596309546465 k: 7
L1: 113.91355996692812 L2: 1155.3097428372687 L1+L2: 634.6116514020985 k: 8
L1: 106.78232923954882 L2: 1411.7657988552594 L1+L2: 759.2740640474041 k: 9
L1: 90.7930659288961 L2: 1853.7375084125592 L1+L2: 972.2652871707277 k: 10

Reference

[1] k-평균 알고리즘