개요

정규화 관련 정보들을 검색하다보면, 단어들이 혼재되어 사용되기 때문에 처음 보거나 오랜만에 보면 헷갈릴 수 있습니다.

또한 사람들마다 조금씩 용어를 다르게 정의하고 있기도 합니다.

이러한 상황에서 혼동되는 용어와 해석의 차이 때문에 헤매게 되는 시간을 줄이고자, 관련 용어와 정의에 대해 큰 틀에서 가볍게 훑고 가 보자는 취지에서 이번 글을 작성하게 되었습니다.

(정규화 방법에 대한 설명과 계산 과정 등 생략 된 부분들은 이후 추가로 업로드 할 예정입니다.)

본문

용어의 일반적인 정의

이번 포스팅에선 Scaling, Standardization, Regularization 에 대해서 짚고 넘어가보도록 하겠습니다.

( Normalization 은 내용이 방대하고, 한번에 너무 많은 내용을 담으면 혼동이 올 수 있어서, 다음 포스팅에서 설명 하려고 합니다. )

Scaling:
일반적으로 데이터의 범위를 임의로 조정하는 것을 의미합니다.
데이터 분포의 모양은 변하지않고 기존 데이터와 동일한 비율을 유지한 채 범위를 조정합니다.

출처: towardsdatascience
Standardization:
일반적으로 평균으로 구한 분포의 표준 편차를 1로 맞추기 위해 데이터를 바꾸는 것을 의미합니다.

각 feature 간의 상대적 거리를 왜곡시킬 수 있는 점을 고려하여 사용해야 합니다.

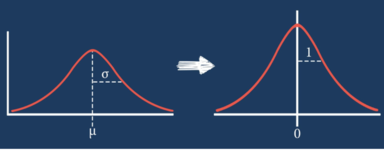
출처: towardsdatascience

Regularization:
일반적으로 가중치를 조정할 때 추가적인 제약을 주는 것을 의미합니다.

용어 설명

Scaling

사용 목적은 아래와 같습니다.

독립된 여러 개의 변수를 사용할 때 각 변수 별로 단위가 다를 경우, 학습 시에 미치는 중요도가 달라지는 문제를 방지할 수 있습니다.

(ex. 키와 나이 변수를 사용할 때, 키 변수가 학습에 더 큰 영향을 끼치는 문제가 발생합니다.)
경사 하강법과 같은 방법론을 사용할 때 수렴 속도를 높여줍니다.
신경망에서 시그모이드 함수와 같은 활성 함수를 사용할 때, saturation현상이 빨리 일어나지 않도록 도와줍니다.

(*참고: saturation 현상 관련 글)
딥러닝에서 Local Minimum에 빠질 위험을 감소 시켜줍니다.

대표적으로 사용하는 기법들은 아래와 같습니다.

Min Max
Max Abs
Robust
Standard

( 그러나 Robust, Standard 두 스케일러의 경우 용어 정리에서 제시한 scaling의 조건을 온전히 충족하지 못합니다. )

Min Max Scaling

: 최소 값은 0 최대 값은 1으로, 모든 데이터가 [0, 1] 범위안에 들어가도록 조절하는 기법입니다.

= Min max normalization, Rescaling, 최소 최대 정규화, Scaling, Normalization

( 협업 할 때 Scaling, Normalization과 같이 포괄적인 단어 사용은 지양하는 것을 추천합니다. )

$x_{new} = \frac{x - x_{min}}{x_{max} - x_{min}}$

적용 예시

import pandas as pd
import matplotlib.pyplot as plt

df = pd.DataFrame([[166, 18],
                  [172, 25],
                  [158, 30],
                  [182, 21],
                  [161, 26],
                  [155, 15]])
df.columns = ['height', 'age']
df_new = (df - df.min())/(df.max() - df.min())

# 시각화
plt.title('Origin Dataset')
plt.plot(df)
plt.legend(df.columns)

plt.title('Scaled Dataset')
plt.plot(df_new)
plt.legend(df_new.columns)

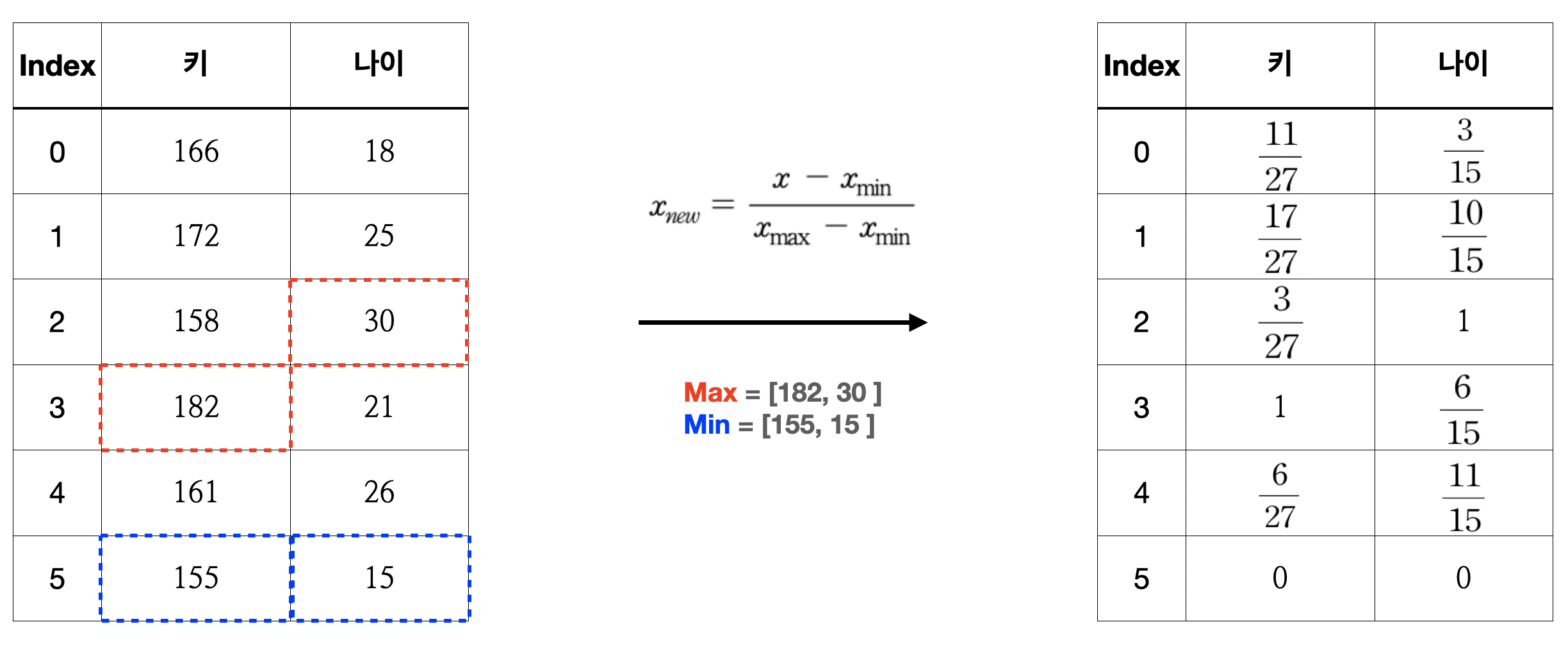
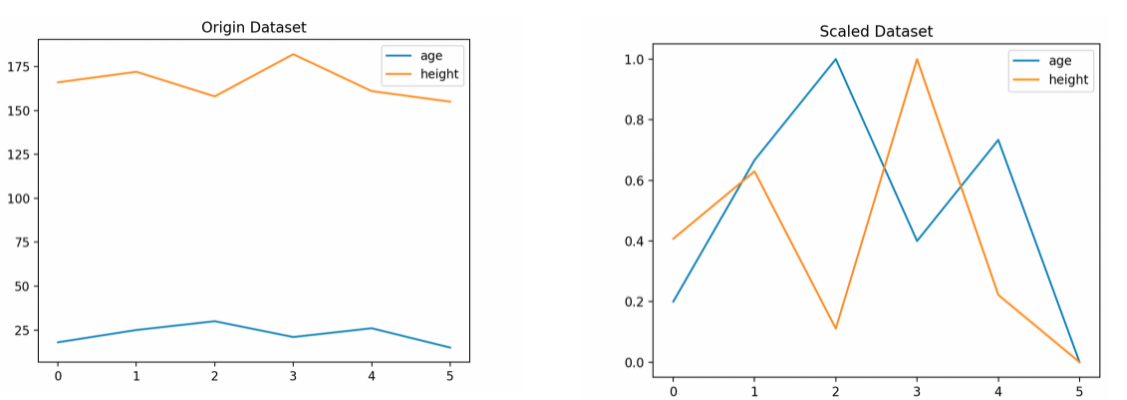
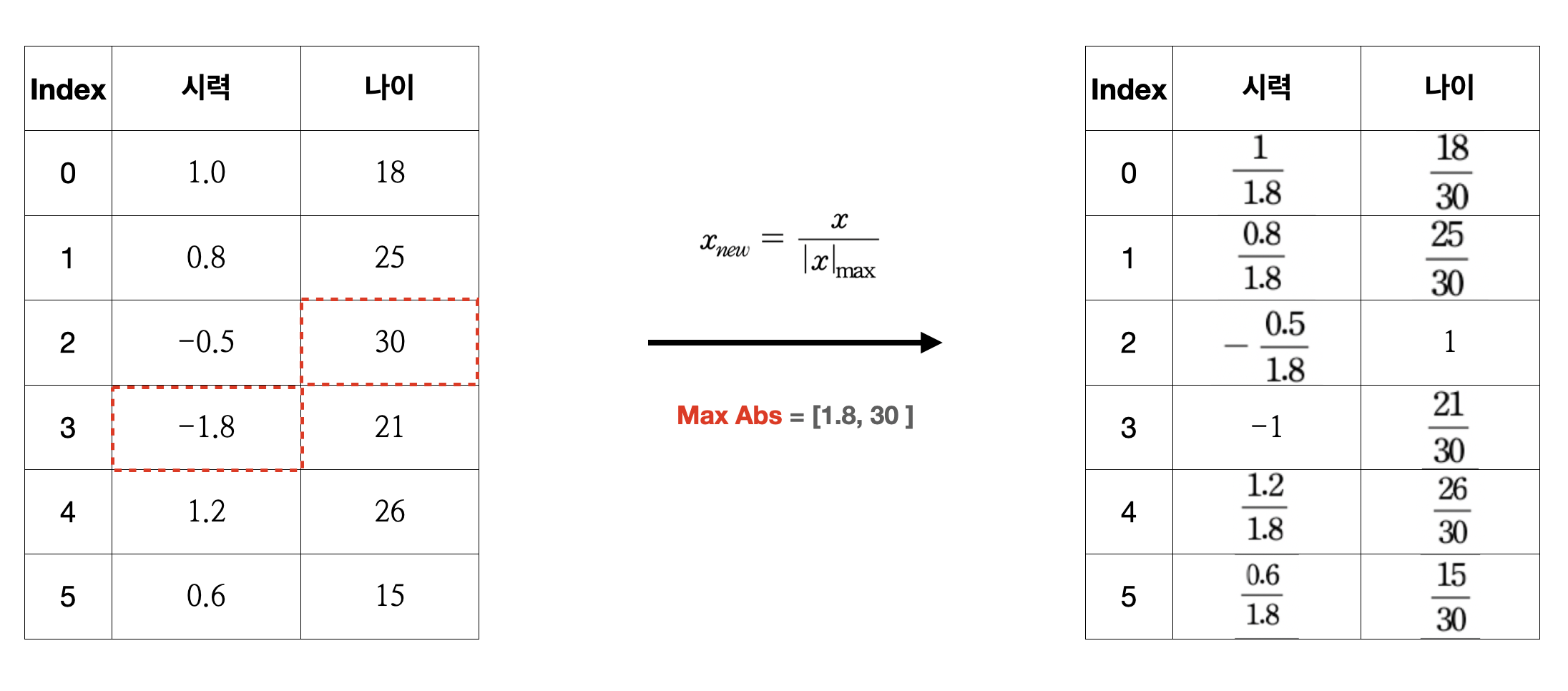
Max Abs

: 절댓값이 가장 큰 수의 절대값으로 전체를 나누어 모든 데이터의 범위를 [-1, 1 ]으로 조절하는 기법입니다.

$x_{new} = \frac{x}{\left\vert x \right\vert_{max}}$

적용 예시

import pandas as pd
import matplotlib.pyplot as plt

df = pd.DataFrame([[1.0, 18],
                  [0.8, 25],
                  [-0.5, 30],
                  [-1.8, 21],
                  [1.2, 26],
                  [0.6, 15]])
df.columns = ['sight', 'age']
df_new = df/df.abs().max()

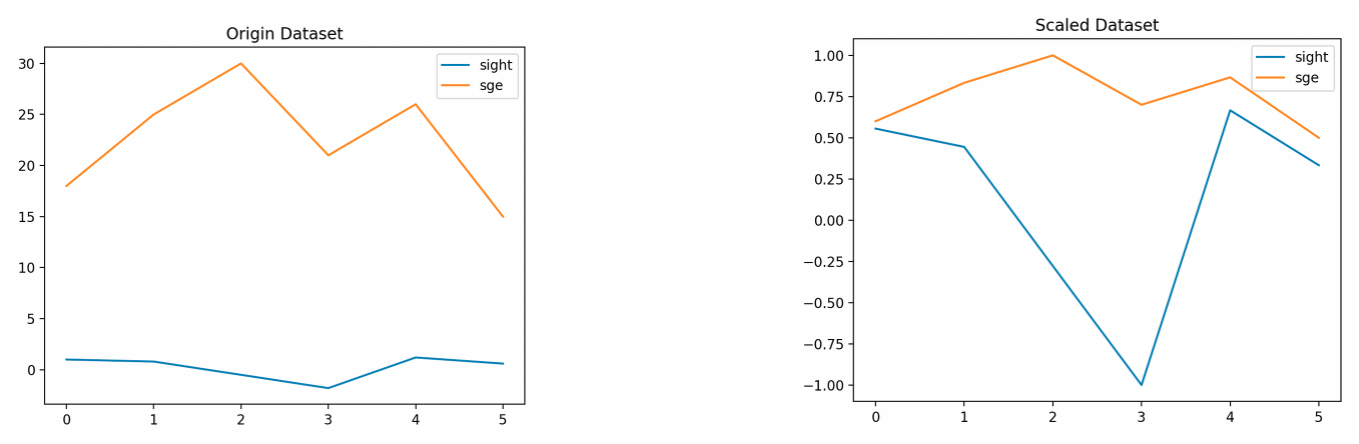
# 시각화
plt.title('Origin Dataset')
plt.plot(df)
plt.legend(df.columns)

plt.title('Scaled Dataset')
plt.plot(df_new)
plt.legend(df_new.columns)

Robust

: 중앙값과 IQR을 활용하여 아웃라이어의 영향을 적게 받는 것이 특징인 기법입니다.

( 단, 미리 결정된 범위로 조정하는 것이 아니기 때문에 앞에서 정의한 Scaling의 조건을 온전히 만족하지 못합니다. )

$x_{new} = \frac{x-x_{median}}{IQR}$

Standard

: 아래의 Z-Score Normalization와 같은 기법입니다.

( Robust와 같은 이유로 scaling이라고 보기에는 어려움이 있고, Standardization으로 구분하여 지칭하는 것을 추천드립니다. )

Standardization

사용 목적은 아래와 같습니다.

정규분포를 표준 정규분포로 변환시켜주어 서로 다른 자료들을 쉽게 비교 분석할 수 있도록 만들어 줍니다.
모든 정규 분포에 대한 확률을 쉽게 구할 수 있습니다.
딥러닝 알고리즘에서 (특히 회귀 타입의 모델을 사용할 때), zero mean and unit variance 데이터를 필요로 하는 경우에도 종종 사용됩니다.

( *참고: why it’s important to give the features zero mean and unit variance? )

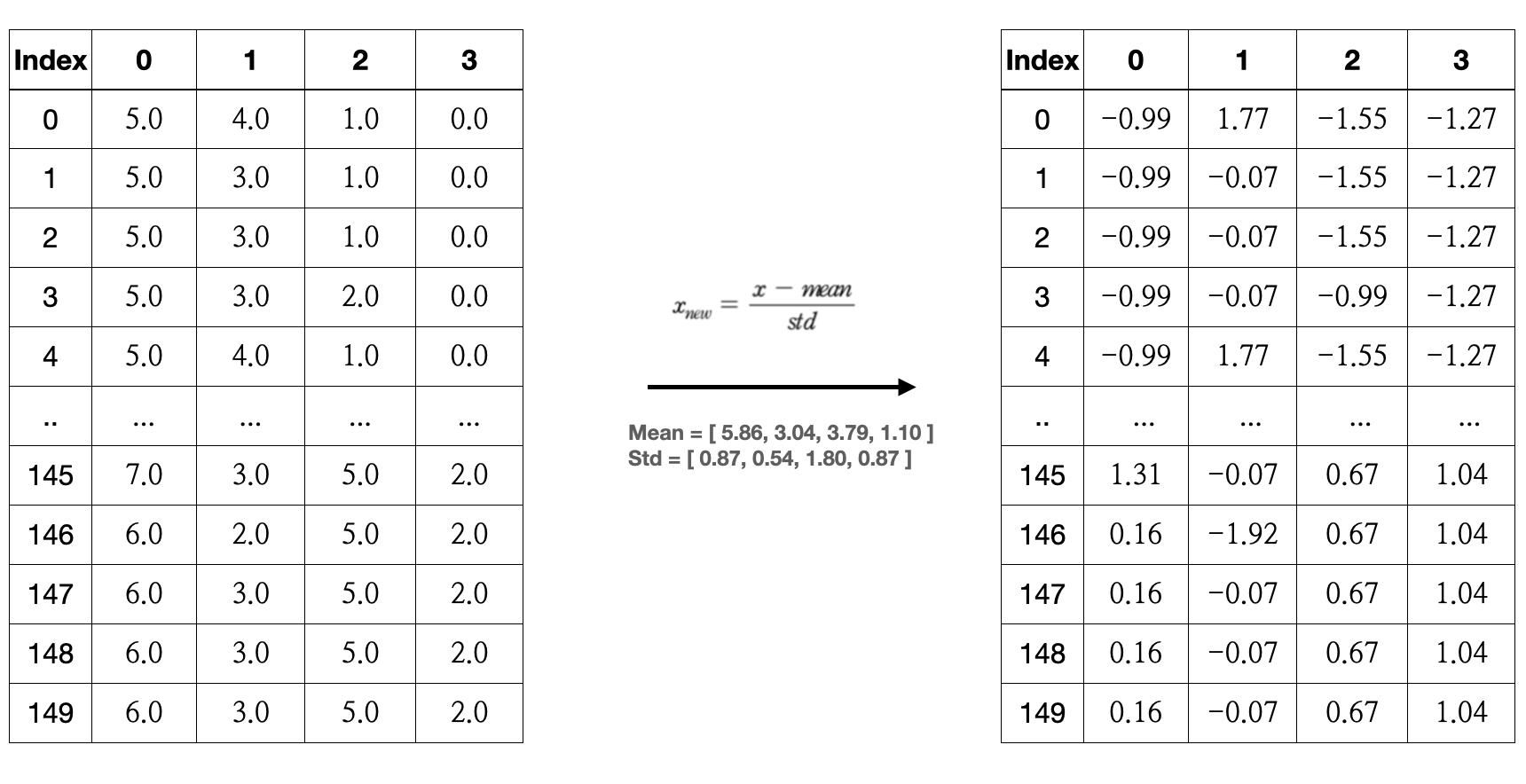
Standardization

: 데이터를 평균 0, 표준편차 1인 표준정규분포로 만들어주는 기법입니다.

= Z-Score Normalization, 표준화, 일반화, Z-점수 정규화

$x_{new} = \frac{x-mean}{std}$

(*참고: z-score 개념 관련 영상)

적용 예시

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

iris_arr = load_iris()
iris_df = pd.DataFrame(iris_arr['data'].round(2))

iris_df_standarded= (iris_df - iris_df.mean())/iris_df.std()

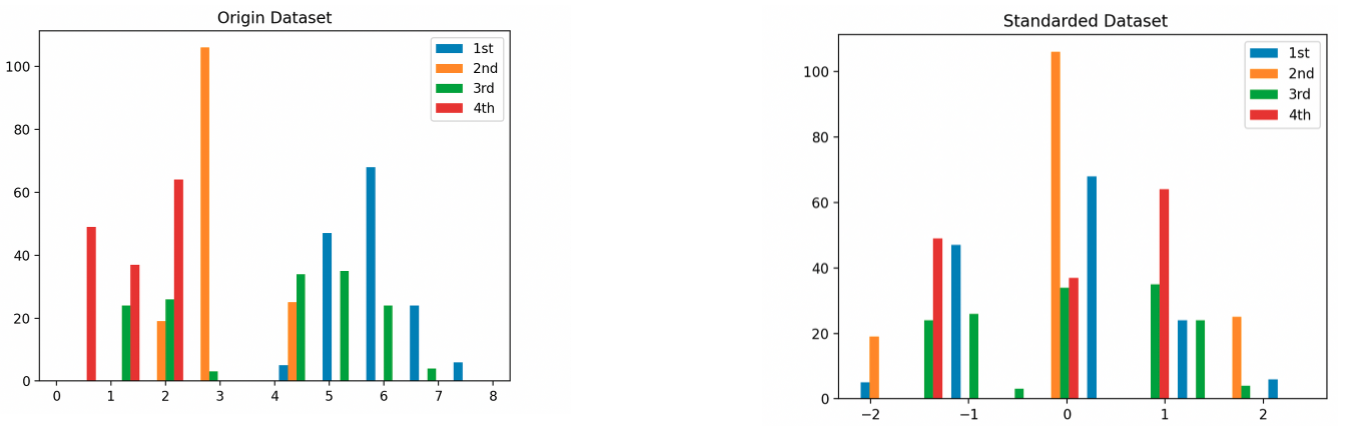
# 시각화
plt.title('Origin Dataset')
plt.hist(iris_df)
plt.legend(iris_df.columns)

plt.title('Standarded Dataset')
plt.hist(iris_df_standarded)
plt.legend(iris_df_standarded.columns)

Regularization

사용 목적은 아래와 같습니다.

학습 데이터에 대한 민감도를 낮춰줍니다.
(결과적으로) 과적합을 방지하기 위해 사용됩니다.

대표적으로 사용하는 기법은 아래와 같습니다.

Ridge
Lasso
Elastic Net

Ridge

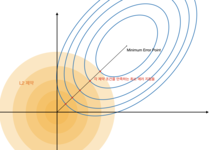
: L2 norm을 사용하여 가중치에 규제를 가하는 기법입니다.

: 가장 일반적으로 사용되는 기법으로, 변수간 상관관계가 높아도 좋은 성능을 보이고, 크기가 큰 변수를 우선적으로 줄이는 것이 특징입니다.

= L2 regularization, L2 정칙화, L2 규제, 릿지, Normalization

( 그러나, Normalization과 같이 포괄적인 단어 사용은 지양하는 것을 추천합니다. )

$f(Cost) = f(Loss) + \Lambda\sum{w}^2$

적용 예시

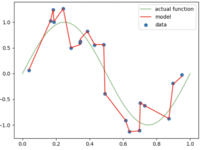
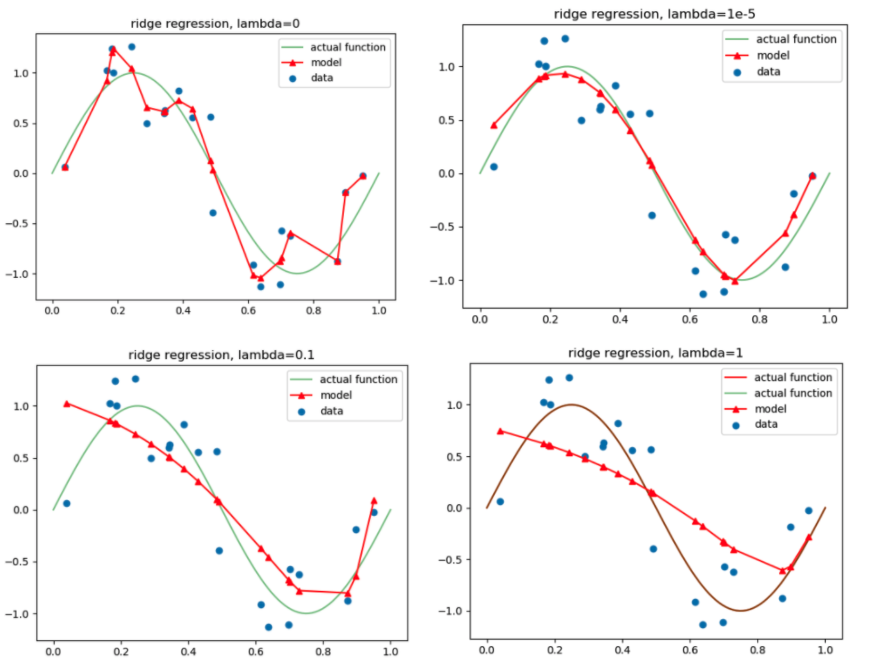
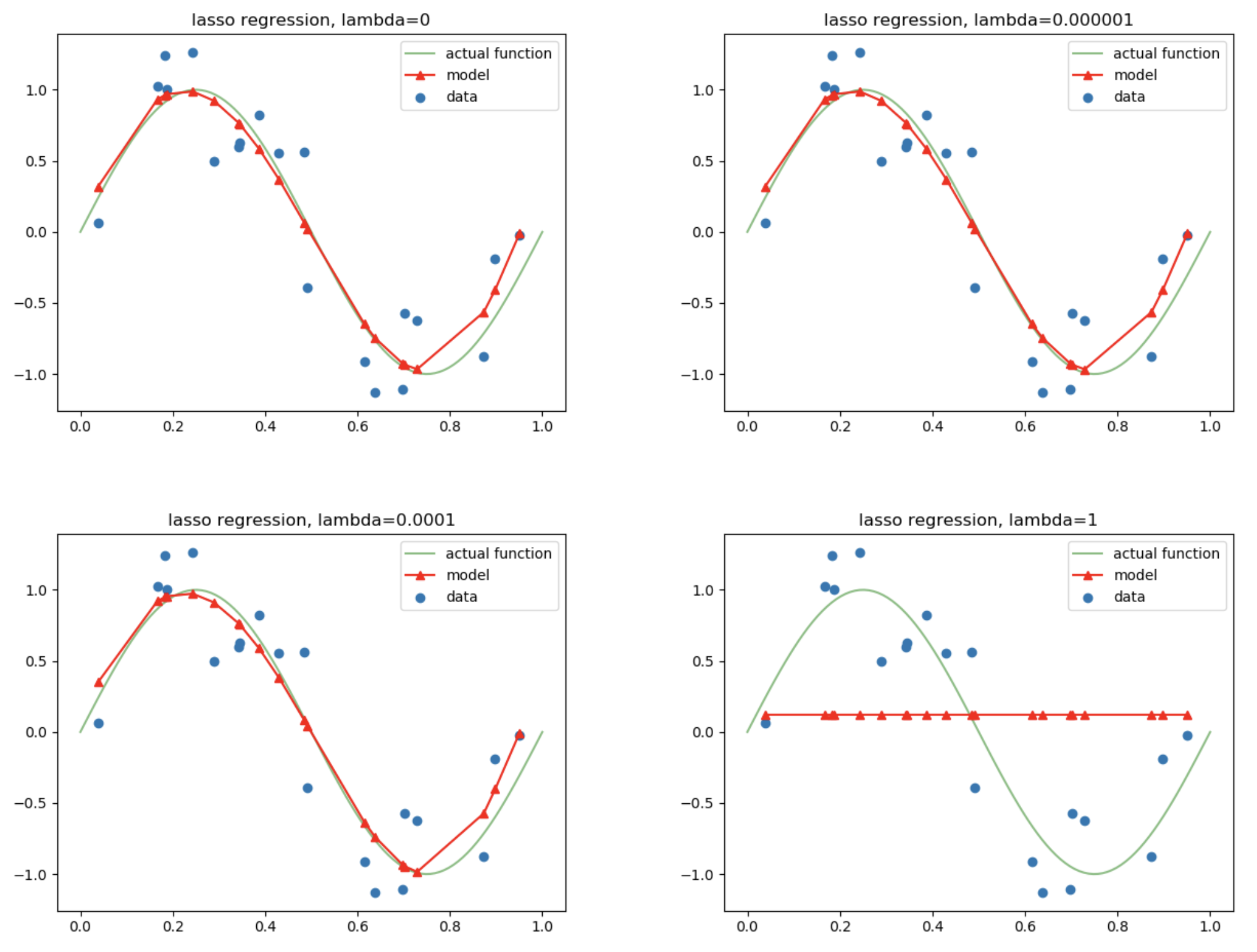
Lasso

: L1 norm을 사용하여 가중치에 규제를 가하는 기법입니다.

: 변수 선택이 가능하고, 비중요 변수를 우선적으로 줄이는 것이 특징입니다.

= L1 regularization, L1 정칙화, L1 규제, 라쏘

$f(Cost) = f(Loss) + \Lambda\sum{\left\vert w \right\vert}$

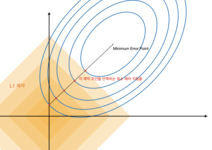
적용 예시

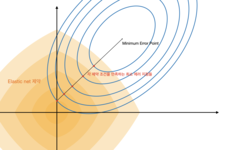
Elastic Net

: Ridge와 Lasso 두 방법론을 혼합한 유형입니다.

: 변수 선택이 가능하고, 상관관계가 큰 변수를 동시에 선택하고 배제 있는 것이 특징입니다.

= 엘라스틱 넷

$f(Cost) = f(Loss) + \Lambda\sum{w^2} + \Lambda\sum{\left\vert w \right\vert}$

적용 예시

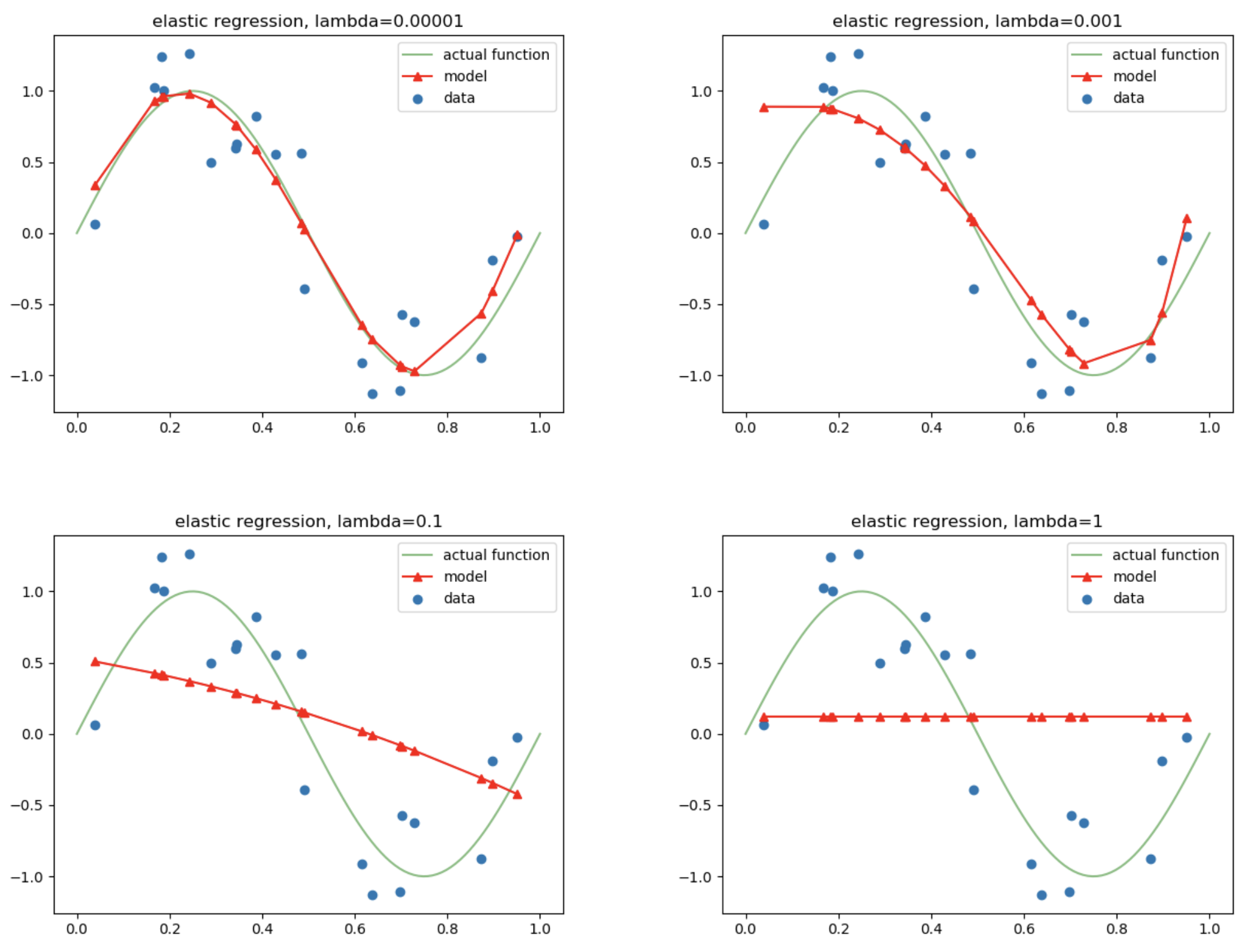
추가적으로 자주 사용되는 Regularization 기법들 아래와 같습니다.

Fused Lasso: 인접한 변수들을 동시에 선택하는 정칙화 기법입니다.
Group Lasso: 사용자가 정의한 그룹 단위로 변수를 선택하는 정칙화 기법입니다.
Graph Constrained Regularization: 사용자가 정의한 그래프의 연결관계에 따라 변수를 선택하는 정칙화 기법입니다.

Reference

https://sebastianraschka.com/Articles/2014_about_feature_scaling.html#about-standardization

https://towardsdatascience.com/scale-standardize-or-normalize-with-scikit-learn-6ccc7d176a02

https://medium.com/@isalindgren313/transformations-scaling-and-normalization-420b2be12300

https://towardsdatascience.com/all-about-feature-scaling-bcc0ad75cb35

https://www.analyticsvidhya.com/blog/2017/06/a-comprehensive-guide-for-linear-ridge-and-lasso-regression/

https://towardsdatascience.com/regularization-the-path-to-bias-variance-trade-off-b7a7088b4577